如图,已知抛物线y= (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
如图,已知抛物线 轴交于点A(-4,0)和B(1,0),与y轴交于C点.
轴交于点A(-4,0)和B(1,0),与y轴交于C点.
(1)求此抛物线的解析式;
(2)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的长最大,并求此时P点的坐标;
(3)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当 的面积是
的面积是 面积的2倍时,求E点的坐标.
面积的2倍时,求E点的坐标.
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
 (1)求证:AB=AC;
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若AB=13,sinB= ,求CE的长.
,求CE的长.
如图:已知A(-4,n)、B(2,-4)是一次函数y1=kx+b的图象与反比例函数y2= 的图象
的图象
的两个交点.
(1)求反比例函数和一次函数的解折式.
(2)求直线AB与x轴的交点C的坐标及△AOB的面积.
(3)求不等式y1<y2 的解集(请直接写出答案).
的解集(请直接写出答案).
如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).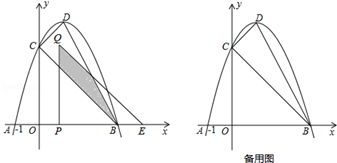
(1)求点B,C的坐标;
(2)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?