(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.
请你仿照小森的思考方式,求出这个八边形的面积.
如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P、Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿A→D方向以每秒1cm的速度运动,到点D停止.P、Q两点用一条可伸缩的细橡皮筋联结,设x秒后橡皮筋扫过的面积为ycm2.当0≤x≤1时,求y与x之间的函数关系式;
当橡皮筋刚好触及钉子时,求x值
当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;
当0≤x≤2时,请在给出的直角坐标系中画出y与x之间的函数图象.

在等腰梯形ABCD中,AD∥BC,AB=DC,且BC=2.以CD为直径作⊙O1交AD于点E,过点E作EF⊥AB于点F.建立如图所示的平面直角坐标系,已知A、B两点坐标分别为A(2,0)、B(0,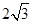 ).
).求C、D两点的坐标;
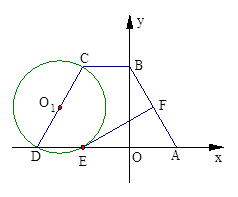
求证:EF为⊙O1的切线
线段CD上是否存在点P,使以点P为圆心,PD为半径的⊙P与y轴相切.如果存在,请求出P点坐标;如果不存在,请说明理由.

某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
| 员工 |
管理人员 |
普通工作人员 |
|||||
| 人员结构 |
总经理 |
部门经理 |
科研人员 |
销售人员 |
高级技工 |
中级技工 |
勤杂工 |
| 员工数(名) |
1 |
3 |
2 |
3 |
 |
24 |
1 |
| 每人月工资(元) |
21000 |
8400 |
2025 |
2200 |
1800 |
1600 |
950 |
请你根据上述内容,解答下列问题:
该公司“高级技工”有名;
所有员工月工资的平均数为2500元,中位数为元,众数为元;
小张到这家公司应聘普通工作人员.
请你回答右图中小张的问题,并指出用⑵中的哪个数据向小张介绍员工的月工资实际水平更合理些;去掉四个管理人员的工资后,请你计
算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.
如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .
用含α的式子表示h(不必指出α的取值范围);
当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?(
 取1.73)
取1.73)