(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
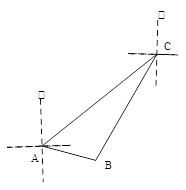
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N(如图1)。
(1)求证:AM=AN;
(2)设BP=x。
①若,BM= ,求x的值;
,求x的值;
②记四边形ADPE与△ABC重叠部分的面积为S,求S与x之间的函数关系式以及S的最小值;
③连接DE,分别与边AB、AC交于点G、H(如图2),当x取何值时,∠BAD=150?并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形,请说明理由。
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2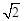 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为.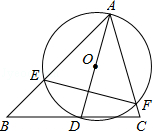
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是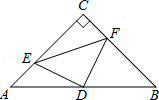
A.1个 B.2个 C.3个 D.4个
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC.CD上滑动,且E、F不与B.C.D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.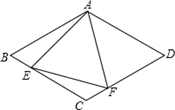
钓鱼岛及其附属岛屿是中国固有领土,A、B、C分别是钓鱼岛、南小岛、黄尾屿上的点(如图),点C在点A的北偏东47°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为5.5km;同时,点B在点C的南偏西36°方向.若一艘中国渔船以30km/h的速度从点A驶向点C捕鱼,需要多长时间到达(结果保留小数点后两位)?(参考数据:sin54°≈0.81,cos54°≈0.59,tan47°≈1.07,tan36°≈0.73,tan11°≈0.19)