如图,一个可以自由转动的均匀转盘被分成了4等份,每份内均标有数字,小明和小亮商定了一个游戏,规则如下:
(1)连续转动转盘两次;
(2)将两次转盘停止后指针所指区域内的数字相加(当指针恰好停在分格线上时视为无效,重转);
(3)若数字之和为奇数,则小明赢;若数字之和为偶数,则小亮赢.
请用“列表”或“画树状图”的方法分析一下,这个游戏对双方公平吗?并说明理由.
张聪与李明为得到一张去上海看世博会的门票,各自设计了一种方案。
张聪:如图是一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张聪得到门票,否则李明得到门票。
李明:将三个完全相同的小球分别标上数字1,2,3后,放入一个不透明袋子中,从中随机取出一个小球,然后放回袋子混合均匀后,再随机取出一个小球,若两次取出的小球上数字之和为偶数,李明得到门票,否则张聪得到门票。
请你运用所学概率的知识,分析张聪和李明的设计方案对双方是否公平。
(本题8分)如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,
(1)△ABC与△EDC相似吗?为什么?(2)求A、B两地间的距离。
(本题8分)二次函数的图象经过点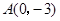 ,
, ,
,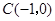 .
.
(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移个单位,使得该图象的顶点在原点.
(本题6分)解方程:4x2-3x-1=0
(本题12分)如图,一抛物线的顶点A为(2,-1),交x轴于B、C(B左C右)两点,交y轴于点D,且B(1,0),坐标原点为O,
(1)求抛物线解析式.
(2)连接CD、BD,在x轴上确定点E,使以A、C、E为顶点的三角形与△CBD相似,并求出点E的坐标.
(3)若点M(m,1)是抛物线上对称轴右侧的一点,点Q也在抛物线上,点P在x轴上,是否存在以O、M、P、Q为顶点的四边形是平行四边形,若存在,请直接写出点P的坐标;若不存在,请说明理由.