已知数列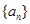 满足
满足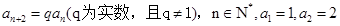 ,且
,且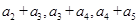 成等差数列.
成等差数列.
(Ⅰ)求q的值和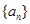 的通项公式;
的通项公式;
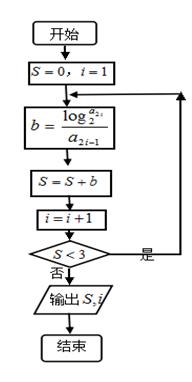
(Ⅱ)若下图所示算法框图中的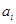 即为(I)中所求,回答以下问题:
即为(I)中所求,回答以下问题:
(1)若记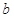 所构成的数列为
所构成的数列为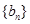 ,求数列
,求数列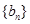 的前
的前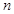 项和
项和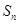
(2)求该框图输出的结果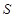 和
和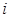
设数列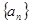 的前
的前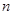 项积为
项积为 ,且
,且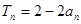 (n∈N*).
(n∈N*).
(1)求 ,并证明:
,并证明: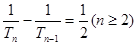 ;
;
(2)设 , 求数列
, 求数列 的前
的前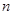 项和
项和 .
.
在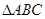 中,角
中,角 所对的边为
所对的边为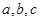 ,已知
,已知 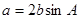 ,
, .
.
(1)求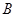 的值;
的值;
(2)若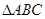 的面积为
的面积为 ,求
,求 的值.
的值.
已知函数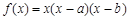 ,点
,点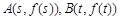 .
.
(1)若 ,函数
,函数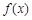 在
在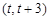 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求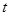 的取值范围;
的取值范围;
(2)当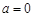 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求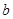 的取值范围;
的取值范围;
(3)若 ,函数
,函数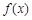 在
在 和
和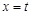 处取得极值,且
处取得极值,且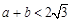 ,
,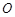 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
如图,已知椭圆C: 的左、右焦点为
的左、右焦点为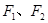 ,其上顶点为
,其上顶点为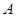 .已知
.已知 是边长为
是边长为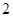 的正三角形.
的正三角形.
(1)求椭圆C的方程;
(2)过点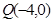 任作一动直线
任作一动直线 交椭圆C于
交椭圆C于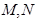 两点,记
两点,记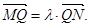 若在线段
若在线段 上取一点
上取一点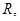 使得
使得 ,试判断当直线
,试判断当直线 运动时,点
运动时,点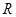 是否在某一定直线上运动?若在请求出该定直线,若不在请说明理由.
是否在某一定直线上运动?若在请求出该定直线,若不在请说明理由.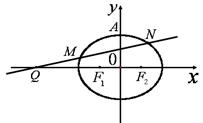
如图,底面 为正三角形,
为正三角形,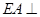 面
面 ,
,  面
面 ,
,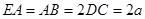 ,设
,设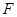 为
为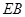 的中点.
的中点.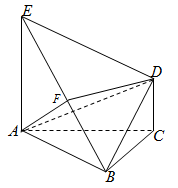
(1)求证: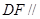 平面
平面 ;
;
(2)求直线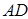 与平面
与平面 所成角的正弦值.
所成角的正弦值.