某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表: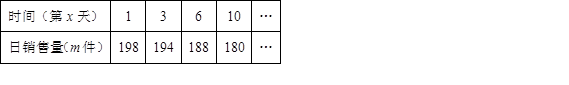
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
把两个相同的正方形剪一剪,拼一拼(这里的剪拼应该是无重叠且无缝隙的),拼成一个大正方形,除了如图所示的方法外,请你再用另一种方法剪拼一下,画出示意图
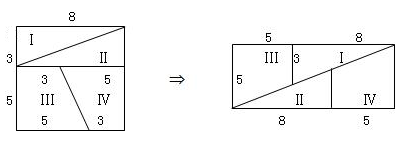
小王把一个边长为8的正方形剪成4块,如下图画成了一个矩形,示意他的拼图方法,你认为这样的拼图方法正确吗?用一句话说明理由
某运输部门规定:办理托运,当一件物品的重量不超过a千克(a<18)时,需付基础费30元和保险费b元;为了限制过重物品的托运,当一件物品超过a千克时,除了付以上基础费和保险费外,超过部分还需每千克付c元的超重费.设某件物品的重量为x千克当0<x≤a时,支付费用为___________(用含b的代数式表示);
当x>a时,支付费用为 ____________(用含x和a、b、c的代数式表示);甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:

①根据以上提供的信息确定a、b、c的值;
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克的物品?若能,请你设计出一种最省的托运方案;若不能,请你说明理由.
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.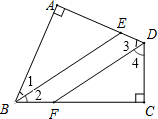
如图,AD为△ABC的中线,BE为△ABD的中线,
若∠ABE=25°,∠BAD=50°,则∠BED的度数是度
在△ADC中过点C画AD边上的高CH.
若△ABC的面积为20,BD=5,求点E到BC边的距离
先化简,再求值: ,其中
,其中 .
.