如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.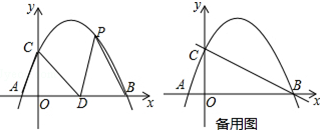
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
我市某养殖场计划购买甲、乙两种鱼苗共700尾,甲种鱼苗每尾3元,乙种鱼苗每尾5元,相关资料表明:甲、乙两种鱼苗的成活率分别为85%和90%.
(1)若购买这两种鱼苗共用去2500元,则甲、乙两种鱼苗各购买多少尾?
(2)若要使这批鱼苗的总成活率不低于88%,则甲种鱼苗至多购买多少尾?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的费用最低?并求出最低费用.
为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.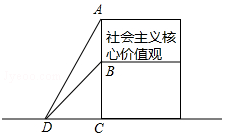
(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:
(1)本次接收随机抽样调查的男生人数为人,扇形统计图中“良好”所对应的圆心角的度数为;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF= AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.