如图①,一次函数 的图象与二次函数
的图象与二次函数 的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
(1)当m=﹣1,n=4时,k= ,b= ;
当m=﹣2,n=3时,k= ,b= ;
(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;
(3)利用(2)中的结论,解答下列问题:如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.
①当m=﹣3,n>3时,求 的值(用含n的代数式表示);
的值(用含n的代数式表示);
②当四边形AOED为菱形时,m与n满足的关系式为 ;
当四边形AOED为正方形时,m= ,n= .
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).
(1)画出△AOB绕点O逆时针旋转90°后得到的△A1OB1.
(2)填空:点A1的坐标为.
(3)求出在旋转过程中,线段OB扫过的扇形面积.
已知:如图,Rt△ABC中,∠C=90°,AC=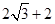 ,BC=
,BC=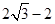 ,
,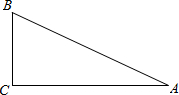
求:
(1)Rt△ABC的面积;
(2)斜边AB的长.
解方程:(1)4x2-9=0 (2)x(x-2)+x-2=0
已知△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E、F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,联结AF、AE,交BD于点G.
(1)如图(1),求证:∠EAF=∠ABD;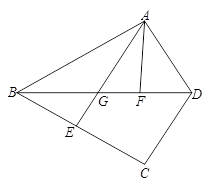
图(1)
(2)如图(2),当AB=AD时,M是线段AG上一点,联结BM、ED、MF,MF的延长线交ED于点N,∠MBF= ∠BAF,AF=
∠BAF,AF=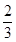 AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.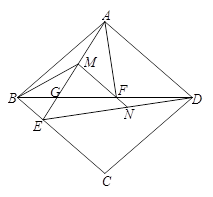
图(2)
已知直线y=kx-3与x轴交于点A(4,0),与y轴交于点C,抛物线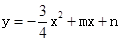 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.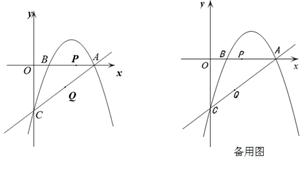
(1)求此抛物线的解析式和直线的解析式;
(2)如果点P和点Q同时出发,运动时间为t(秒),试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相似;
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.