(本小题满分12分)某工厂生产 两种元件,其质量按测试指标
两种元件,其质量按测试指标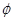 划分为:
划分为: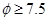 为正品,
为正品,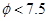 为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
 |
9 |
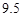 |
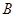 |
6 |
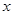 |
 |
 |
 |
由于表格被污损,数据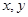 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 两种元件的检测数据的平均数相等,方差也相等.
两种元件的检测数据的平均数相等,方差也相等.
(1)求表格中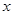 与
与 的值;
的值;
(2)若从被检测的5件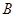 种元件中任取2件,求取出的2件都为正品的概率.
种元件中任取2件,求取出的2件都为正品的概率.
如图, 在直三棱柱 ABC - A1B1C1中, D、 E分别是BC和CC1的中点, 已知AB=AC=AA1=4,∠BAC=90°.
(Ⅰ)求证: B1D⊥平面AED;
(Ⅱ)求二面角B1-AE-D的余弦值;
(Ⅲ)求三棱锥A-B1DE的体积.
已知数列{an}的前n项和为Sn, 且满足a1 = 2, nan + 1 = Sn + n(n + 1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列 }的前n项和, 求Tn;
}的前n项和, 求Tn;
(Ⅲ)设 , 证明:
, 证明:
选修4-5: 不等式选讲
已知函数 f (x)=" |x" - 2|,g(x)=" -|x" + 3| +m.
(Ⅰ)若关于x的不等式 g(x)≥0的解集为 [-5, -1], 求实数m的值;
(Ⅱ)若 f (x)的图象恒在 g(x)图象的上方, 求实数m的取值范围.
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C( ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈  , 直线
, 直线 的参数方程为
的参数方程为 为参数), 直线
为参数), 直线 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
(本小题满分10分)选修4-5:不等式选讲
已知实数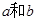
 ,若不等式
,若不等式 有解,记实数M的最小值为m.
有解,记实数M的最小值为m.
(1)求m的值;
(2)解不等式 .
.