如图,在边长为1的小正方形网格中,三角形的三个顶点均落在格点上.
(1)以三角形的其中两边为边画一个平行四边形,并在顶点处标上字母A,B,C,D;
(2)证明四边形ABCD是平行四边形.
已知自变量 与因变量 的对应关系如表呈现的规律.
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
12 |
11 |
10 |
9 |
8 |
|
(1)直接写出函数解析式及其图象与 轴和 轴的交点 , 的坐标;
(2)设反比例函数 的图象与(1)求得的函数的图象交于 , 两点, 为坐标原点且 ,求反比例函数解析式;已知 ,点 与 分别在反比例函数与(1)求得的函数的图象上,直接写出 与 的大小关系.
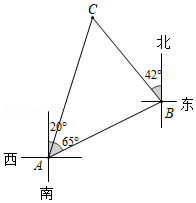
如图,一艘船由 港沿北偏东 方向航行 到 港,然后再沿北偏西 方向航行至 港,已知 港在 港北偏东 方向.
(1)直接写出 的度数;
(2)求 、 两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)
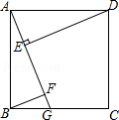
如图,正方形 , 是 边上任意一点(不与 、 重合), 于点 , ,且交 于点 .
(1)求证: ;
(2)四边形 是否可能是平行四边形,如果可能,请指出此时点 的位置,如不可能,请说明理由.
(1)计算: ;
(2)已知 是小于0的常数,解关于 的不等式组: .
如图1,抛物线 交 轴于 , 两点,其中点 的坐标为 ,与 轴交于点 .
(1)求抛物线的函数解析式;
(2)点 为 轴上一点,如果直线 与直线 的夹角为 ,求线段 的长度;
(3)如图2,连接 ,点 在抛物线上,且满足 ,求点 的坐标.
