如图，抛物线y=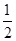
x2+bx+c经过A（-1，0），C（2，-3）两点，与y轴交于点D，与x轴交于另一点B．
（1）求此抛物线的解析式及顶点坐标；
（2）若将此抛物线平移，使其顶点为点D，需如何平移？写出平移后抛物线的解析式；
（3）过点P（m，0）作x轴的垂线（1≤m≤2），分别交平移前后的抛物线于点E，F，交直线OC于点G，求证：PF=EG．
观察下表，填表后再解答问题
（1）试完成下列表格
| 序号 |
1 |
2 |
3 |
n |
| ●●● ●☆● ●●● |
●●●●● ● ☆☆ ● ● ☆☆ ● ● ● ●●●●● |
●●●●●●● ●☆☆☆ ● ●☆☆☆ ● ●☆☆☆ ● ● ● ● ● ●●●●●●● |
/ |
|
| ●个数 |
8 |
24 |
||
| ☆个数 |
1 |
4 |
（2）试求第几个图形中，“●”的个数和“☆”个数相等﹒
如图，长阳公园有四棵树，A、B、C、D（单位：米）
（1）请写出A、B两点坐标﹒
（2）为了更好的保护古树，公园决定将如图所示的四边形用围栏圈起来，划为保护区，请你计算保护区面积﹒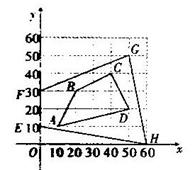
如图，这是某市部分简图，为了确定各建筑物的位置：
（1）请你以火车站为原点建立平面直角坐标系﹒
（2）写出超市的坐标（小正方形网格的单位长度为1）﹒
（3）请将体育场、宾馆和火车站看作三点，用线段连接起来，得到△ABC，然后将此三角形向下平移4个单位，再画出平移后的△A′B′C′，并计算△A′B′C′的面积﹒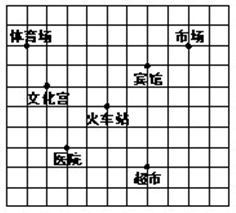
如图，已知∠1+∠2=180°，∠DEF=∠A，∠BED=60°，求∠ACB的度数﹒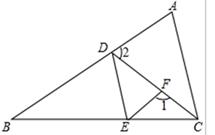
（1）9x2–25=0
（2）(x+5)3=–27
（3）
（4）