(本小题满分12分)学校生活区内建有一块矩形休闲区域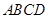 ,
, ,
, ,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路
,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路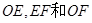 ,考虑到学校整体规划,要求
,考虑到学校整体规划,要求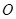 是
是 的中点,点
的中点,点 在边
在边 上,点
上,点 在边
在边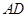 上,且
上,且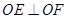 如图所示.
如图所示.
(1)设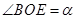 ,试将
,试将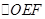 的周长
的周长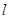 表示成
表示成 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
如图,在平面直角坐标系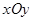 中,点
中,点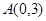 ,直线
,直线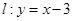 。设圆
。设圆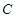 的半径为
的半径为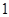 ,圆心在
,圆心在 上。
上。
(1)若圆心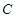 也在直线
也在直线 上,过点
上,过点 作圆
作圆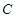 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆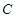 上存在点
上存在点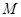 ,使
,使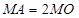 ,求圆心
,求圆心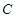 的横坐标
的横坐标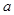 的取值范围。
的取值范围。
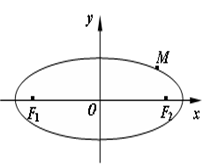
如图,在平面直角坐标系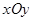 中,已知椭圆
中,已知椭圆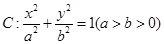 经过点
经过点
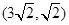 ,椭圆的离心率
,椭圆的离心率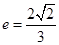 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作两直线与椭圆
作两直线与椭圆 分别交于相异两点
分别交于相异两点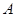 、
、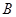 .若
.若 的平分线与
的平分线与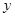 轴平行, 试探究直线
轴平行, 试探究直线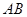 的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由.
的斜率是否为定值?若是, 请给予证明;若不是, 请说明理由.
在等比数列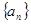 中,
中, ,
,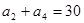
(1) 和公比
和公比 ;
;
(2)前6项的和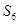 .
.
设命题 ;命题
;命题 :不等式
:不等式 对任意
对任意 恒成立.若
恒成立.若 为真,且
为真,且 或
或 为真,求
为真,求 的取值范围.
的取值范围.
求经过直线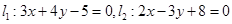 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:
(1)与直线2x+3y+5=0平行;
(2)与直线2x+3y+5=0垂直.