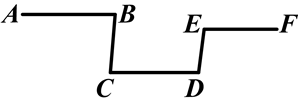
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5 个单位.直线l从与AC重合的位置开始,以每秒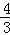 个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动
个单位的速度沿CB方向平行移动,即移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动

(1)①当t=3秒时,点P走过的路径长为 ;②当t= 秒时,点P与点E重合;③当t= 秒时,PE∥AB;
(2)当点P在AC边上运动时,将△PEF绕点E逆时针旋转,使得点P的对应点M落在EF上,点F的对应点记为点N,当EN⊥AB时,求t的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点,记为点Q.在点P与直线l运动的过程中,若形成的四边形PEQF为菱形,请直接写出t的值.
如图所示,△ABC平移后得到了△DEF,D在AB上,若∠A=26°,∠E=74°,求∠1,∠2,∠F,∠C的度数.
阅读:如图1所示,因为CE∥AB,所以∠1=∠A,∠2=∠B,所以∠ACD=∠1+∠2=∠A+∠B,这是一个有用的事实.请用这个结论在如图2所示的四边形ABCD内过点D引一条和边AB平行的直线,求∠A+∠B+∠C+∠ADC的度数.
如图所示,把一张长方形纸片ABCD沿EF折叠后,ED与BC的交点为G,D,C分别落在D′,C′的位置上,若∠EFG=55°,求∠1与∠2的度数.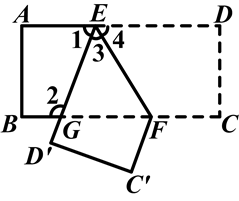
如图所示,已知AB∥CD,∠B=140°,∠D=150°,求∠E的度数.
如图所示,AB∥CD∥EF,BC∥ED,∠E=100°,求∠B的度数.