(本小题满分12分)某体育赛事组委会为确保观众顺利进场,决定在体育场外临时围建一个矩形观众候场区,总面积为 (如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为
(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为 的入口.现已知铁栏杆的租用费用为100元
的入口.现已知铁栏杆的租用费用为100元 .设该矩形区域的长为
.设该矩形区域的长为 (单位:
(单位: ),租用铁栏杆的总费用为
),租用铁栏杆的总费用为 (单位:元)
(单位:元)
(Ⅰ)将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定 ,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
(本小题满分12分)已知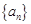 是公差不为零的等差数列,且
是公差不为零的等差数列,且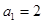 ,
, ,
,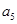 ,
,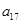 成等比数列.
成等比数列.
(1)求数列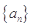 的通项公式;
的通项公式;
(2)设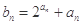 ,求数列
,求数列 的前
的前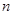 项和
项和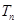 .
.
(本小题满分10分)选修4-5:不等式选讲
设函数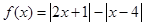 .
.
(1)解不等式: ;
;
(2)若 对一切实数
对一切实数 均成立,求
均成立,求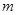 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系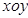 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(
,(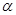 为参数),以原点
为参数),以原点 为极点,
为极点,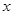 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为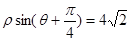 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线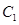 上的动点,求点
上的动点,求点 到
到 上点的距离的最小值.
上点的距离的最小值.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径, 是弧
是弧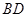 的中点,
的中点, ,垂足为
,垂足为 ,
,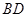 交
交 于点
于点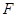 .
.
(1)求证: ;
;
(2)若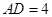 ,⊙
,⊙ 的半径为6,求
的半径为6,求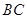 的长.
的长.
(本小题满分12分)已知函数 (
( 为自然对数的底数),曲线
为自然对数的底数),曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.