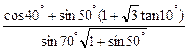(本小题满分12分)甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(Ⅰ)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(Ⅱ)若左右手依次各取两球,称同一手中 两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列和数学期望.
((本小题满分12分)
现将边长为2米的正方形铁片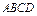 裁剪成一个半径为1米的扇形
裁剪成一个半径为1米的扇形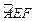 和一个矩形
和一个矩形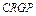 ,如图所示,点
,如图所示,点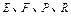 分别在
分别在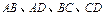 上,点
上,点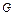 在
在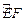 上.设矩形
上.设矩形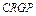 的面积为
的面积为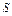 ,
, ,试将
,试将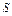 表示为
表示为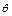 的函数,并指出点
的函数,并指出点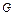 在
在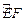 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.
((本小题满分12分)
由倍角公式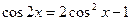 ,可知
,可知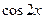 可以表示为
可以表示为 的二次多项式.
的二次多项式.
对于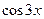 ,我们有
,我们有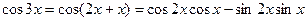
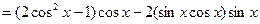
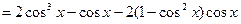

可见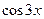 可以表示为
可以表示为 的三次多项式。一般地,存在一个
的三次多项式。一般地,存在一个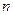 次多项式
次多项式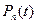 ,使得
,使得 ,这些多项式
,这些多项式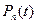 称为切比雪夫多项式.
称为切比雪夫多项式.
(I)求证: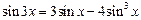 ;
;
(II)请求出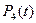 ,即用一个
,即用一个 的四次多项式来表示
的四次多项式来表示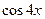 ;
;
(III)利用结论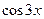
 ,求出
,求出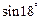 的值.
的值.
((本小题满分12分)
已知函数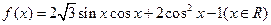 .
.
(I)求函数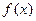 的最小正周期及在区间
的最小正周期及在区间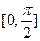 上的最大值和最小值;
上的最大值和最小值;
(II)若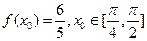 ,求
,求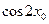 的值.
的值.
(本小题满分12分)
已知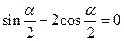 ,求:
,求:
(I) 的值;
的值;
(II) 的值;
的值;
(III)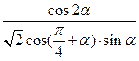 的值.
的值.
(本小题满分10分)
求值: