如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.
(1)求证:四边形AFCE是菱形;
(2)若AB=3,AD=4,求菱形AFCE的边长.
如图,△ABC与△ADE中,∠C=∠E,∠1=∠2.求证:DE:BC=AE:AC.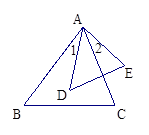
二次函数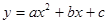 的图象过点A(3,0),B(-1,0)且与y轴交点为C(0,6).
的图象过点A(3,0),B(-1,0)且与y轴交点为C(0,6).(1)此二次函数的解析式;
(2)求三角形ABC的面积;
(3)若点D位于x轴上方的抛物线上,当△ABD的面积取得最大值时,求D点的坐标.
已知二次函数y= x2 -4x+3.(1)用配方法将y= x2 - 4x+3化成y=a (x-h) 2 +k的形式;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)写出当x为何值时,y>0.
(4)写出当
 时,直接写出相应y的取值范围.
时,直接写出相应y的取值范围.
如图,已知△ABC顶点的坐标分别为A(1,-1),B(4,-1),C(3,-4).
(1)将△ABC绕点A逆时针旋转90°后,得到△AB1C1.在所给的直角坐标系中画出旋转后的
 ,并写出点
,并写出点 的坐标:
的坐标: ____________;
____________;(2)以坐标原点O为位似中心,在第二象限内再画一个放大的
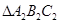 ,使得它与△ABC的位似比等于2:1 .
,使得它与△ABC的位似比等于2:1 .
如图,对称轴为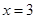 的抛物线
的抛物线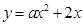 与
与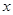 轴相交于点
轴相交于点 、
、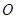 .
.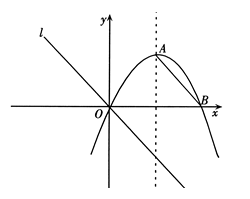
求抛物线的解析式,并求出顶点
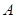 的坐标;
的坐标;连结AB,把AB所在的直线平移,使它经过原点O,得到直线l.点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
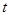 ,当0<S≤18时,求
,当0<S≤18时,求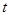 的取值范围;
的取值范围;在(2)的条件下,当
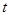 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点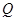 ,使△OP
,使△OP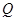 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点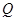 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.