如图所示,已知点C(-3,m),点D(m-3,0).直线CD交y轴于点A.作CE与X轴垂直,垂足为E,以点B(-1,0)为顶点的抛物线恰好经过点A、C.

(1)则∠CDE= ;
(2)求抛物线对应的函数关系式;
(3)设P(x,y)为抛物线上一点(其中-3<x<1-或-1<x<1,连结BP并延长交直线CE于点N,记N点的纵坐标为yN,连结CP并延长交X轴于点M.
①试证明:EM•(EC+yN)为定值;
②试判断EM+EC+yN是否有最小值,并说明理由
已知 求
求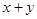 的算术平方根.
的算术平方根.
(1)解方程: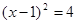
(2)解方程组:
如图(1),抛物线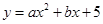 (
( )与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为
)与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为 ,抛物线的对称轴与
,抛物线的对称轴与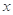 轴交于点E,点D(-2,-3)在对称轴上.
轴交于点E,点D(-2,-3)在对称轴上.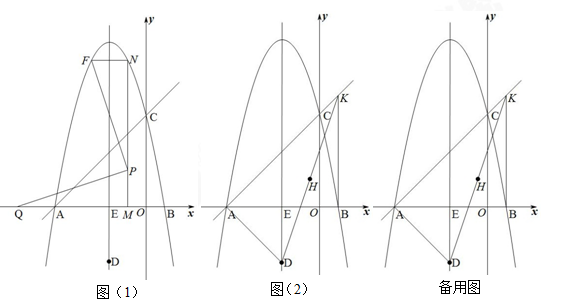
(1)求此抛物线的解析式;
(2)如图(1),若点M是线段OE上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;
(3)如图(2),过点B作BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿GH边翻折得△DGH,求当KG为何值时,△DGH与△KGH重叠部分的面积是△DGK面积的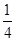 .
.
阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A( ,B
,B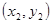 ,AB中点P的坐标为
,AB中点P的坐标为 .由
.由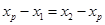 ,得
,得 ,同理
,同理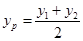 ,所以AB的中点坐标为(
,所以AB的中点坐标为(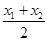 ,
,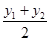 ).由勾股定理得
).由勾股定理得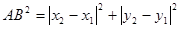 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=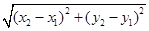 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l: 与抛物线
与抛物线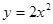 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.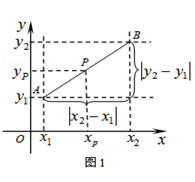
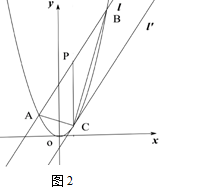
(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF.
(1)若∠DAB=15°,AB=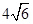 ,求线段AD的长度.
,求线段AD的长度.
(2)求证:∠EFB=∠CDA.