甲乙两地相距400km，一辆轿车从甲地出发，以一定的速度匀速驶往乙地．0．5h后，一辆货车从乙地出发匀速驶往甲地（轿车的速度大于货车的速度），与轿车在途中相遇．此后，两车继续行驶，并各自到达目的地．两车之间的距离y（km）与轿车行驶的时间x（h）的函数图象如图．
（1）解释D点的实际意义并求两车的速度；
（2）求m、n的值；
（3）若两车相距不超过180千米时能够保持联系，请问货车在行驶过程中与轿车保持联系的时间有多长？
在△ABC中，AD是△ABC的角平分线．
（1）如图1，过C作CE∥AD交BA延长线于点E，若F为CE的中点，连结AF，求证：AF⊥AD；
（2）如图2，M为BC的中点，过M作MN∥AD交AC于点N，若AB=4， AC=7，
求NC的长．
已知：一次函数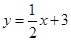
的图象与正比例函数
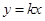的图象相交于点
A（a，1）．
（1）求a的值及正比例函数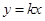的解析式；
（2）点P在坐标轴上（不与点O重合），若PA=OA，直接写出P点的坐标；
（3）直线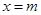
与一次函数的图象交于点B，与正比例函数图象交于点C，若△ABC的面积记为S，求S关于m的函数关系式（写出自变量的取值范围）．
阅读下列材料：
木工张师傅在加工制作家具的时候，用下面的方法在木板上画直角：
如图1，他首先在需要加工的位置画一条线段AB，接着分别以点A、点B为圆心，以大于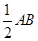
的适当长为半径画弧，两弧相交于点C，再以C为圆心，以同样长为半径画弧交AC的延长线于点D（点D需落在木板上），连接DB．则∠ABD就是直角．
木工张师傅把上面的这种作直角的方法叫做“三弧法．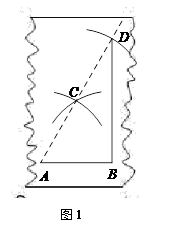
解决下列问题：
（1）利用图1就∠ABD是直角作出合理解释 (要求：先写出已知、求证，再进行证明)；
（2）图2表示的一块残缺的圆形木板，请你用“三弧法”，在木板上画出一个以EF为一条直角边的直角三角形EFG（要求：尺规作图，不写作法，保留作图痕迹）．
如图，直线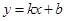
经过点A（0，5），B（1，4）．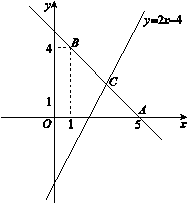
（1）求直线AB的解析式；
（2）若直线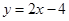
与直线AB相交于点C,求点C的坐标；
（3）根据图象，写出关于x的不等式2x－4≥kx+b的解集．
已知：如图， A、B、C、D四点在同一直线上，AB=CD，AE∥BF且AE=BF．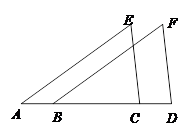 
求证： EC=FD．