某居民小区内建有一块矩形草坪ABCD，AB=50米，BC=25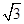
米，为了便于居民平时休闲散步，该小区物业管理公司将在这块草坪内铺设三条小路OE，EF和OF，考虑到小区整体规划，要求O是AB的中点，点E在边BC上，点F在边AD上，且OE⊥OF，如图所示．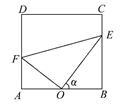
（1）设∠BOE=α，试将△OEF的周长l表示成α的函数关系式，并求出此函数的定义域．
（2）经核算，三条路每米铺设费用均为400元．试问如何设计才能使铺路的总费用最低?并求出最低总费用．
（本小题满分12分）已知数列
的前
项和为
，且满足
。
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，数列
的前项和为
，求证：
。
（本小题满分12分）已知数列
中，
,数列
满足
。
（1）求证：数列是等差数列；
（2）求数列中的最大项和最小项，并说明理由。
（本小题满分12分）设函数
。（Ⅰ）求函数
的最小正周期；（Ⅱ）若函数
的图像与函数
的图像关于原点对称，求
的值。
在直角坐标系xoy中，以o为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为
，M,N分别为C与x轴，y轴的交点
（1）写出C的直角坐标方程，并求出M,N的极坐标；
（2）设MN的中点为P，求直线OP的极坐标方程.
设函数
．
（1）解不等式
；
（2）若关于的不等式
的解集不是空集，试求
的取值范围．