(本小题满分10分)已知全集 ,集合
,集合 ,集合
,集合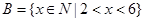 .
.
求(1) ;
;
(2) .
.
(本题满分6分)
已知圆锥的正视图是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的侧面积;
(Ⅱ)经过圆锥的高AO的中点O¢作平行于圆锥底面的截面,
求截得的两部分几何体的体积比.
(本题满分10分)
已知抛物线 上横坐标为
上横坐标为 的点
的点 到焦点
到焦点 的距离为
的距离为 .
.
(I)求抛物线的方程;
(II)若斜率为 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且点
两点,且点 在直线
在直线 的右上方,求证:△
的右上方,求证:△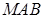 的内心在直线
的内心在直线 上;
上;
(III)在(II)中,若 ,求
,求 的内切圆半径长.
的内切圆半径长.
(本题满分10分)
已知椭圆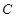 的方程为
的方程为 ,称圆心在坐标原点
,称圆心在坐标原点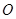 ,半径为
,半径为 的圆为椭圆
的圆为椭圆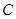 的“伴随圆”,椭圆
的“伴随圆”,椭圆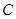 的短轴长为2,离心率为
的短轴长为2,离心率为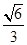 .
.
(Ⅰ)求椭圆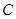 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若直线 与椭圆
与椭圆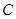 交于
交于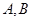 两点,与其“伴随圆”交于
两点,与其“伴随圆”交于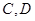 两点,当
两点,当 时,求△
时,求△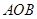 面积的最大值.
面积的最大值.
(本题满分9分)
如图所示的多面体中,已知直角梯形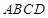 和矩形
和矩形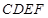 所在的平面互相垂直,
所在的平面互相垂直,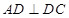 ,
,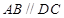 ,
,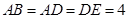 ,
, .
.
(Ⅰ)证明: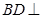 平面
平面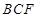 ;
;
(Ⅱ)设二面角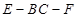 的平面角为
的平面角为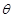 ,求
,求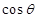 的值;
的值;
(Ⅲ)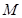 为
为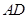 的中点,在
的中点,在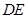 上是否存在一点
上是否存在一点 ,使得
,使得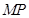 ∥平面
∥平面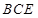 ?若存在,求出
?若存在,求出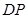 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.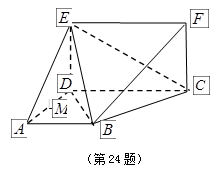
(本题满分8分)
已知经过点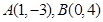 的圆
的圆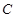 与圆
与圆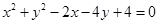 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线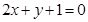 .
.
(Ⅰ)求圆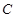 的方程;
的方程;
(Ⅱ)若动圆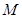 经过一定点
经过一定点 ,且与圆
,且与圆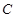 外切,求动圆圆心
外切,求动圆圆心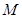 的轨迹方程.
的轨迹方程.