(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的直径,C,F是圆O上的两点,AF//OC,过C作圆O的切线交AF的延长线于点D.
(Ⅰ)证明: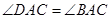 ;
;
(Ⅱ)若 ,垂足为M,求证:AM·MB=DF·DA.
,垂足为M,求证:AM·MB=DF·DA.
已知函数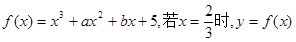 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.
(1)求函数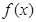 的解析式;
的解析式;
(2)求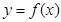 在
在 上的最大值和最小值.
上的最大值和最小值.
已知抛物线的顶点是双曲线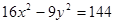 的中心,而焦点是双曲线的顶点,求抛物线的方程.
的中心,而焦点是双曲线的顶点,求抛物线的方程.
(本小题满分14分)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)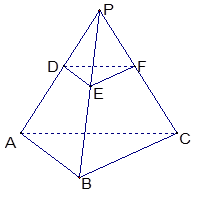
(1)求证:P-ABC为正四面体;
(2)棱PA上是否存在一点M,使得BM与面ABC所成的角为45°?若存在,求出点M的位置;若不存在,请说明理由。
(3)设棱台DEF-ABC的体积为V=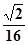 , 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
, 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
(本小题满分14分)
已知棱长为1的正方体ABCD-A1B1C1D1中,P在对角线A1C1上,记二面角P-AB-C为α,二面角P-BC-A为β。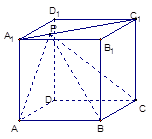
(1)当A1P:PC1=1:3时,求cos(α+β)的大小。
(2)点P是线段A1C1(包括端点)上的一个动点,问:当点P在什么位置时,α+β有最小值?
(本小题满分12分)
如图,四棱锥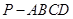 中,
中,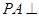 底面
底面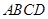 ,四边形
,四边形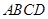 中,
中, 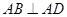 ,
,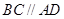 ,
, 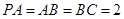 ,
,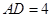 ,E为
,E为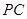 中点.
中点.
(1)求证:CD⊥面PAC;(2)求:异面直线BE与AC所成角的余弦值;