(本小题满分10分)在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsin(θ+ )=
)= a,曲线C2的参数方程为
a,曲线C2的参数方程为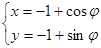 (φ为参数,0≤φ≤π).
(φ为参数,0≤φ≤π).
(1)求C1的直角坐标方程;
(2)当C1与C2有两个不同公共点时,求实数a的取值范围.
(本小题满分14分)已知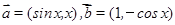 ,
,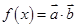 且
且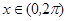 ,记
,记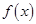 在
在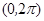 内零点为
内零点为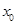 .
.
(1)求当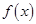 取得极大值时,
取得极大值时,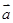 与
与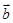 的夹角θ.
的夹角θ.
(2)求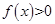 的解集.
的解集.
(3)求当函数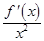 取得最小值时
取得最小值时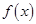 的值,并指出向量
的值,并指出向量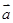 与
与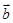 的位置关系.
的位置关系.
(本小题满分12分)已知抛物线方程为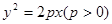
(1)若点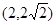 在抛物线上,求抛物线的焦点
在抛物线上,求抛物线的焦点 的坐标和准线
的坐标和准线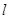 的方程;
的方程;
(2)在(1)的条件下,若过焦点 且倾斜角为
且倾斜角为 的直线
的直线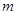 交抛物线于
交抛物线于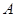 、
、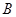 两点,点
两点,点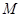 在抛物线的准线
在抛物线的准线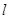 上,直线
上,直线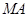 、
、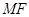 、
、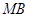 的斜率分别记为
的斜率分别记为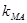 、
、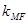 、
、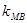 ,
,
求证: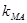 、
、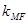 、
、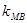 成等差数列;
成等差数列;
(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱.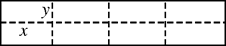
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米时,可使总造价最低?
如图,在侧棱垂直于底面的三棱柱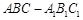 中,
中,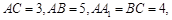 点
点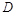 是
是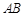 的中点.
的中点.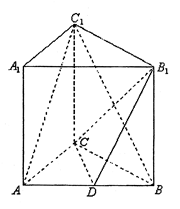
(Ⅰ)求证: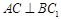 ;
;
(Ⅱ)求证: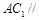 平面
平面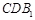 ;
;
(Ⅲ)求三棱锥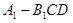 的体积.
的体积.
(本小题满分12分)已知数列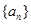 的前
的前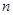 项和为
项和为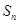 ,且
,且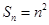 .数列
.数列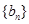 为等比数列,且
为等比数列,且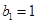 ,
,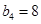 .
.
(Ⅰ)求数列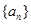 ,
,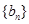 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 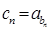 ,求数列
,求数列 的前
的前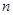 项和
项和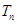 ,并证明
,并证明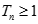 .
.