广安市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)样本中最喜欢B项目的人数百分比是________,其所在扇形图中的圆心角的度数是____;
(2)请把统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
如图,将三角形ABC绕点O旋转得到三角形A/B/C/,且∠AOB=300,∠AOB/=200,则
(1)点B的对应点是________________;
(2)线段OB的对应线段是____________;
(3)∠AOB的对应角是________________;
(4)三角形ABC旋转的角度是__________;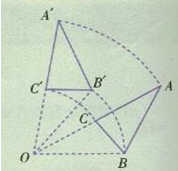
先化简再求值 ,其中x=﹣1.(本题6分)
,其中x=﹣1.(本题6分)
因式分解或解方程组(每小题5分,共10分)
(1) (2)
(2)
如图,△ABC的边BC在直线 上,AC⊥BC,且AC=BC,△EFP的边FP也在直线
上,AC⊥BC,且AC=BC,△EFP的边FP也在直线 上,边EF与边AC重合,且EF=FP。
上,边EF与边AC重合,且EF=FP。
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线 向左平移到图2的位置时,EP交AC于点Q,连结AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想。
向左平移到图2的位置时,EP交AC于点Q,连结AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想。
如图①是一个长方形ABCD,点P按B→C→D→A方向运动,开始时,以每秒2个单位长度匀速运动,到达C点后,改为每秒a个单位匀速运动,到达D后,改为每秒b个单位匀速运动,在整个运动过程中,三角形ABP的面积S与运动时间t的函数关系如图所示。
求:
(1)AB、BC的长;
(2)a,b的值。