某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩（百分制）如下表：
| 候选人 |
面试 |
笔试 |
||
| |
形体 |
口才 |
专业水平 |
创新能力 |
| 甲 |
86 |
90 |
96 |
92 |
| 乙 |
92 |
88 |
95 |
93 |
（1）若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照4：6：5：5的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？
（2）若公司根据经营性质和岗位要求认为：面试成绩中形体占15%，口才占20%，笔试成绩中专业水平占40%，创新能力占25%，那么你认为该公司应该录取谁．
计算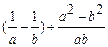
解方程组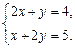
已知抛物线y＝ax2＋bx＋c经过A（－4，3）、B（2，0）两点，当x=3和x=－3时，这条抛物线上对应点的纵坐标相等．经过点C（0，－2）的直线l与 x轴平行，O为坐标原点．
（1）求直线AB和这条抛物线的解析式；
（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；
（3）设直线AB上的点D的横坐标为－1，P（m，n）是抛物线y＝ax2＋bx＋c上的动点，当△PDO的周长最小时，求四边形CODP的面积．
如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．
（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若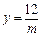
，要使△DEF为等腰三角形，m的值应为多少？
小沈准备给小陈打电话，由于保管不善，电话本上的小陈手机号码中，有两个数字已模糊不清．如果用x、y表示这两个看不清的数字，那么小陈的手机号码为139x370y580（手机号码由11个数字组成），小沈记得这11个数字之和是20的整数倍．
（1）求x+y的值；
（2）求小沈一次拨对小陈手机号码的概率．