如图,△ABC为等边三角形.O为BC的中垂线AH上的动点,⊙O经过B,C两点,D为弧上一点,D,A两点在BC边异侧,连接AD,BD,CD.
(1)如图1,若⊙O经过点A,求证:BD+CD=AD;
(2)如图2,圆心O在BD上,若∠BAD=45°;求∠ADB的度数;
(3)如图3,若AH=OH,求证:BD2+CD2=AD2.
操作:如图①,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角: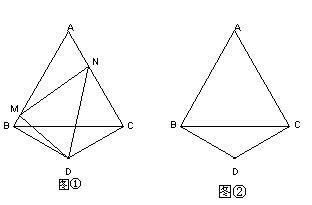
(1)角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
(2)若角的两边分别交AB、CA的延长线于M、N两点,连接MN。在图②中画出图形,再直接写出线段BM、MN、NC之间的关系.
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量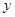 (单位:个)与销售单价
(单位:个)与销售单价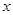 (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示: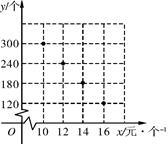
(1)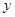 与
与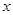 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润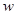 (单位:元)与销售单价
(单位:元)与销售单价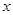 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
先化简:先化简,再求值: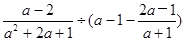 ,其中
,其中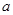 是方程
是方程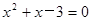 的解.
的解.
解方程:(1)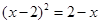
(2)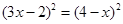 .
.
已知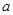 、
、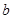 、
、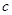 为实数,且
为实数,且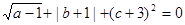 ,求方程
,求方程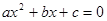 的根.
的根.