(本小题共13分)对于数列 ,若满足
,若满足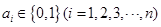 ,则称数列
,则称数列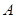 为“0-1数列”.定义变换
为“0-1数列”.定义变换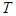 ,
,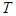 将“0-1数列”
将“0-1数列”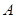 中原有的每个1都变成0,1,原有的每个0都变成1,0.例如
中原有的每个1都变成0,1,原有的每个0都变成1,0.例如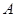 :1,0,1,则
:1,0,1,则 设
设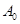 是“0-1数列”,令
是“0-1数列”,令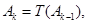
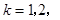 3,….
3,….
(Ⅰ) 若数列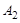 :
: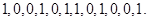 求数列
求数列 ;
;
(Ⅱ) 若数列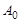 共有10项,则数列
共有10项,则数列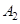 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若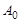 为0,1,记数列
为0,1,记数列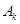 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为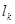 ,
,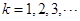 .求
.求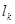 关于
关于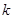 的表达式.
的表达式.
(本题14分)已知向量m = ,向量n =
,向量n = ,且m与n所成角为
,且m与n所成角为 ,其中A、B、C是
,其中A、B、C是 的内角。
的内角。
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围。
的取值范围。
若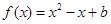 ,且
,且 ,
,
(1)求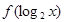 的最小值及相应 x的值;
的最小值及相应 x的值;
(2)若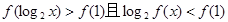 ,求x的取值范围.
,求x的取值范围.
已知函数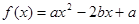 (
(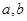
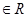 )
)
(1)若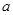 从集合
从集合 中任取一个元素,
中任取一个元素, 从集合
从集合 中任取一个元素,求方程
中任取一个元素,求方程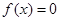 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 从区间
从区间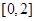 中任取一个数,
中任取一个数,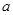 从区间
从区间 中任取一个数,求方程
中任取一个数,求方程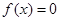 没有实根的概率.
没有实根的概率.
某车间为了规定工时定额,需要确定加共某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?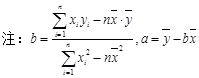
已知函数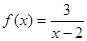 .
.
(1)判断该函数在区间(2,+∞)上的单调性,并给出证明;
(2)求该函数在区间[3,6]上的最大值和最小值.