将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M,连接BF与EG交于点P.
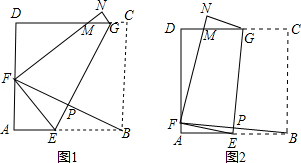
(1)当点F与AD的中点重合时(如图1):
①△AEF的边AE= cm,EF= cm,线段EG与BF的大小关系是EG BF;(填“>”、“=”或“<”)
②求△FDM的周长.
(2)当点F在AD边上除点A、D外的任意位置时(如图2):
③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;
④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?
一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D ,连接AE.(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.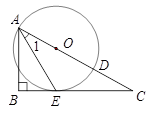
某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题:
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2中所对的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年酸牛奶的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?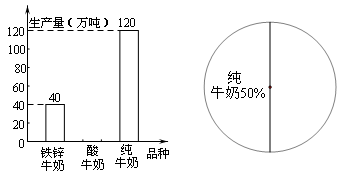
已知等腰△ABC的顶角∠A=36°(如图).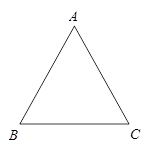
(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)通过计算说明△ABD和△BDC都是等腰三角形.
求不等式组 的整数解.
的整数解.