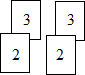
探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
如图,在矩形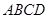 中,把点
中,把点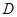 沿AE对折,使点
沿AE对折,使点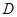 落在
落在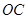 上的
上的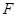 点,已知
点,已知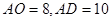 .
.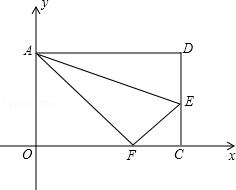
(1)求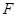 点的坐标;
点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点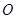 ,
,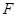 ,且直线
,且直线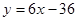 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)直线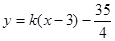 与(2)中的抛物线交于
与(2)中的抛物线交于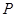 、
、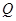 两点,点
两点,点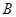 的坐标为
的坐标为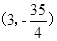 ,求证:
,求证: 为定值.
为定值.
如图1,在平面直角坐标系中, 为坐标原点,
为坐标原点, 是反比例函数
是反比例函数
 图象上任意一点,以
图象上任意一点,以 为圆心,
为圆心,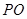 为半径的圆与坐标轴分别交于点
为半径的圆与坐标轴分别交于点 、
、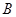 .
.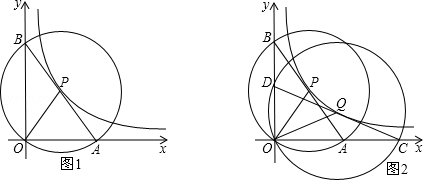
(1)求证:线段AB为⊙P的直径;
(2)求 的面积;
的面积;
(3)如图2, 是反比例函数
是反比例函数
 图象上异于点
图象上异于点 的另一点,以
的另一点,以 为圆心,
为圆心, 为半径画圆与坐标轴分别交于点
为半径画圆与坐标轴分别交于点 、
、 .求证:
.求证: .
.
某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元 ,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
如图,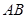 为
为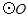 的直径,点
的直径,点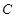 为
为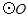 上一点,若
上一点,若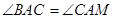 ,过点
,过点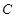 作直线
作直线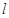 垂直于射线
垂直于射线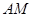 ,垂足为点
,垂足为点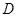 .
.
(1)试判断 与
与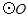 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线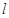 与
与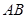 的延长线相交于点
的延长线相交于点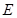 ,
,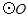 的半径为3,并且
的半径为3,并且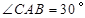 .求
.求 的长.
的长.
小明和小刚做纸牌游戏,如图,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各抽取一张,称为一次游戏.当两张牌的牌面数字之积为奇数,小明得2分,否则小刚得1分,这个游戏对双方公平吗?请说明理由.