如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)判断点C(﹣1,4)是否在该函数图象上.
将Rt△ABC和Rt△DEF按图1摆放(点F与点A重合),点A、E、F、B在同一直线上,∠ACB=∠DEF=90°,∠BAC=∠D=30°,BC=8cm,EF=6cm.
如图2,△DEF从图1位置出发,以1cm/s的速度沿射线AB下滑,DE与AC相交于点H,DF与AC相交于点G,设下滑时间为t(s)(0<t≤6).
(1)当t为何值时,点G在线段AE的垂直平分线上?
(2)是否存在某一时刻t,使B、C、D三点在同一条直线上,若存在,求出t的值;若不存在,请说明理由;
(3)设△DEF与△ABC的重合部分的面积为S,直接写出S与t之间的函数关系式以及S的最大值(不需要给出解答过程).


如图1,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若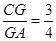 ,求
,求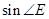 的值.
的值.
(1)已知一元二次方程 的两根为
的两根为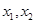 ,求证
,求证 ,
, .
.
(2)已知关于x的一元二次方程 的两个不相等实数根
的两个不相等实数根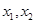 满足
满足 ,求a的值.
,求a的值.
(3)已知抛物线 与x轴交于A.B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,
与x轴交于A.B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时, 取得最小值,并求出最小值.
取得最小值,并求出最小值.
某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件.假设2013年到2015年这种产品产量的年增长率相同.
(1)求2013年到2015年这种产品产量的年增长率;
(2)2014年这种产品的产量应达到多少万件?
某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图.
(1)将图补充完整;
(2)本次共抽取员工 人,每人所创年利润的众数是 ,平均数是 ;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?