(本小题满分14分)已知函数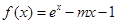
．
（1）当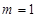
时，试判断函数
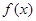的单调性；
（2）对于任意的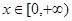
，
恒成立，求
的取值范围．
如图所示，四边形ABCD为矩形，BC⊥平面ABE，F为CE上的点，且BF⊥平面ACE.
(1)求证：AE⊥BE.
(2)设点M为线段AB的中点，点N为线段
本题满分12分）
已知数列
满足
，它的前
项和为
，且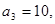
．
①求通项
，
②若
，求数列
的前项和的最小值．
（本小题满分12分） 已知
的周长为
，且
．
（1）求边长
的值；
（2）若
，求
的值．
（本小题满分14分）设关于
的函数
的最小值为
，试确定满足
的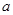
的值，并对此时的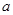值求
的最大值。
（本小题满分13分）有一批单放机原价为每台80元，两个商场均有销售，为了吸引顾客，两商场纷纷推出优惠政策。甲商场的优惠办法是：买一台减4元，买两台每台减8元，买三台每台减12元，......,依此类推，直到减到半价为止；乙商场的优惠办法是：一律7折。某单位欲为每位员工买一台单放机，问选择哪个商场购买比较划算？