如图所示,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE.
(2)设点M为线段AB的中点,点N为线段
已知数列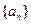 中,
中,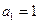 ,
,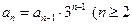 且
且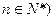
(1)求数列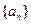 的通项公式;
的通项公式;
(2)设函数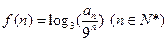 ,数列
,数列 的前
的前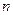 项和为
项和为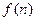 ,求
,求 的通项公式;
的通项公式;
(3)求数列 的前
的前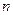 项和
项和 。
。
已知二次函数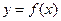 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为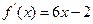 ,数列
,数列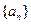 的前n项和为
的前n项和为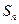 ,点
,点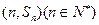 均在函数
均在函数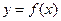 的图像上。
的图像上。
(1)求数列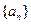 的通项公式;
的通项公式;
(2)设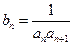 ,
,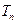 是数列
是数列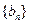 的前n项和,求使得
的前n项和,求使得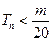 对所有
对所有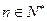 都成立的最小正整数m;
都成立的最小正整数m;
某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管等其它费用为平均每吨每天3元,购面粉每次需支付运费900元.求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
已知数列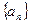 的前
的前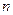 项和
项和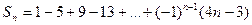 ,
,
(1)求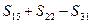 的值。(2)求
的值。(2)求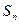 的表达式
的表达式
已知 、
、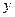 满足约束条件
满足约束条件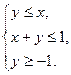
(1)求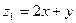 的最小值,以及相应的
的最小值,以及相应的 、
、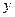 值;
值;
(2)求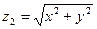 的最大值,以及相应的
的最大值,以及相应的 、
、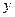 值
值