（本小题共14分）已知抛物线P：x2="2py" （p>0）．
（Ⅰ）若抛物线上点
到焦点F的距离为
．
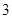（ⅰ）求抛物线
的方程；
（ⅱ）设抛物线的准线与y轴的交点为E，过E作抛物线的切线，求此切线方程；
（Ⅱ）设过焦点F的动直线l交抛物线于A，B两点，连接
，
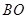并延长分别交抛物线的准线于C，
D两点，求证：以CD为直径的圆过焦点F．
已知
是椭圆
的两个焦点，
为坐标原点，点
在椭圆上，且
，⊙是以
为直径的圆，直线
：
与⊙相切，并且与椭圆交于不同的两点
（1）求椭圆的标准方程；
（2）当
，且满足
时，求弦长
的取值范围.
已知函数
，
.
（1）求函数
的最小值；
（2）若存在
（
是自然对数的底数）使不等式
成立，求实数
的取值范围.
如图所示，已知点
是抛物线
上一定点，直线AM、BM的斜率互为相反数，且与抛物线另交于A、B两个不同的点.
（1）求点M到其准线的距离；
（2）求证：直线AB的斜率为定值.
已知等差数列
的公差
，
，且
成等比数列.
（1）求通项公式
；
（2）令
，
，求数列
的前
项的和
.
已知函数
．
（1）求
的单调递增区间；
（2）当
时，求的值域．