(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为( ,
, ),记∠COA=α.
),记∠COA=α.
(Ⅰ)求 的值;
的值;
(Ⅱ)求cos∠COB的值.
如图,正四棱柱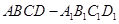 中,
中,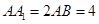 ,点
,点 在
在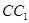 上且
上且 .
.
(Ⅰ)证明: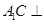 平面
平面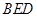 ;
;
(Ⅱ)求二面角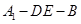 的大小.
的大小.
一个口袋中有大小相同的2个白球和4个黑球,每次从袋中随机地摸出1个球,并换入1只相同大小的黑球,这样继续下去,求:
(I)摸2次摸出的都是白球的概率;
(II)第3次摸出的是白球的概率。
已知函数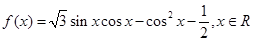 . (Ⅰ) 求函数
. (Ⅰ) 求函数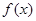 的最小值和最小正周期;(Ⅱ)已知
的最小值和最小正周期;(Ⅱ)已知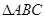 内角
内角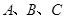 的对边分别为
的对边分别为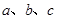 ,且
,且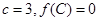 ,若向量
,若向量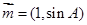 与
与 共线,求
共线,求 的值.
的值.
(本题满分14分)已知函数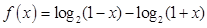 .
.
(1)求函数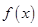 的定义域;
的定义域;
(2)判断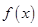 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根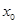 ,请求出一个长度为
,请求出一个长度为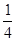 的区间
的区间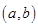 ,使
,使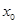
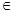
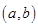 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
.已知圆C: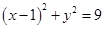 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.