已知数列{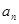 }满足
}满足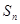 +
+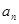 =2n+1 (
=2n+1 ( )
)
(1)求出 ,
,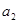 ,
,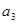 的值;
的值;
(2)由(1)猜想出数列{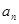 }的通项公式
}的通项公式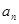 ,并用数学归纳法证明.
,并用数学归纳法证明.
如图所示,扇形AOB,圆心角AOB的大小等于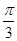 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.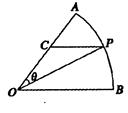
(1)若C是半径OA的中点,求线段PC的长;
(2)设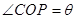 ,求
,求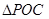 面积的最大值及此时
面积的最大值及此时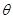 的值.
的值.
设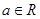 ,函数
,函数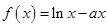 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数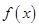 的单调区间;
的单调区间;
(3)当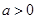 时,求函数
时,求函数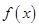 在
在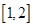 上的最小值.
上的最小值.
已知椭圆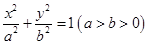 的离心率为
的离心率为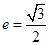 ,直线
,直线 与以原点为圆心、椭圆
与以原点为圆心、椭圆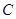 的短半轴长为半径的圆
的短半轴长为半径的圆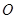 相切.
相切.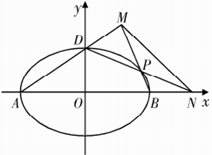
(1)求椭圆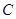 的方程;
的方程;
(2)如图,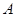 、
、 、
、 是椭圆
是椭圆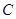 的顶点,
的顶点, 是椭圆
是椭圆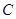 上除顶点外的任意点,直线
上除顶点外的任意点,直线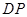 交
交 轴于点
轴于点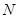 ,直线
,直线 交
交 于点
于点 ,设
,设 的斜率为
的斜率为 ,
, 的斜率为
的斜率为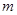 ,求证:
,求证: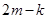 为定值.
为定值.
在数列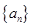 中,
中,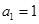 ,
,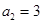 ,
,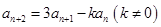 对任意
对任意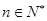 成立,令
成立,令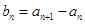 ,且
,且 是等比数列.
是等比数列.
(1)求实数 的值;
的值;
(2)求数列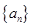 的通项公式;
的通项公式;
(3)求和: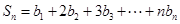 .
.
如图,已知矩形 中,
中,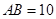 ,
, ,将矩形沿对角线
,将矩形沿对角线 把
把 折起,使
折起,使 移到
移到 点,且
点,且 在平面
在平面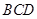 上的射影
上的射影 恰好在
恰好在 上.
上.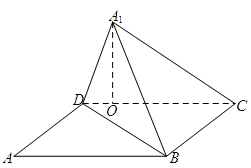
(1)求证: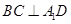 ;
;
(2)求证:平面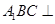 平面
平面 ;
;
(3)求三棱锥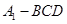 的体积.
的体积.