如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(1)求证:CD⊥PD;
(2)求证:EF∥平面PAD.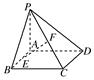
已知双曲线2x2-2y2=1的两个焦点为F1,F2,P为动点,若|PF1|+|PF2|=4.
(1)求动点P的轨迹E的方程;
(2)求cos∠F1PF2的最小值.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
(1)求椭圆的方程;
(2)求m的取值范围;
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且·=·.
(1)求动点P的轨迹C的方程;
(2)过点F的直线交轨迹C于A,B两点,交直线l于点M,已知=λ1,=λ2,求λ1+λ2的值.
物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,且|AB|=.
(1)求抛物线的方程;
(2)在x轴上是否存在一点C,使△ABC为正三角形?若存在,求出C点的坐标;若不存在,请说明理由.