(本小题满分12分)口袋中装有质地大小完全的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号。如果两个编号的和为偶数就算甲胜,否则算乙胜。
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由。
(选修4-4:坐标系与参数方程)
在极坐标系中,设圆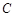 经过点
经过点 ,圆心是直线
,圆心是直线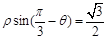 与极轴的交点,求圆
与极轴的交点,求圆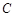 的
的
极坐标方程.
(选修4-2:矩阵与变换)
若点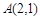 在矩阵
在矩阵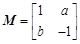 对应变换的作用下得到点
对应变换的作用下得到点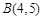 ,求矩阵
,求矩阵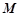 的逆矩阵.
的逆矩阵.
(选修4-1:几何证明选讲)
如图,设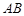 、
、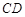 是圆
是圆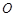 的两条弦,直线
的两条弦,直线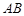 是线段
是线段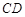 的垂直平分线.已知
的垂直平分线.已知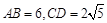 ,求线段
,求线段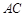 的长度.
的长度.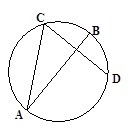
(本小题满分16分)设数列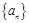 的前
的前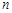 项和为
项和为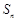 ,满足
,满足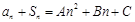
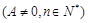 .
.
(1)当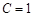 时,
时,
①设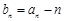 ,若
,若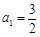 ,
, .求实数
.求实数 的值,并判定数列
的值,并判定数列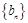 是否为等比数列;
是否为等比数列;
②若数列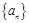 是等差数列,求
是等差数列,求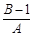 的值;
的值;
(2)当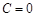 时,若数列
时,若数列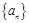 是等差数列,
是等差数列,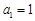 ,且
,且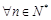 ,
,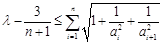 ,
,
求实数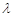 的取值范围.
的取值范围.
(本小题满分16分)已知函数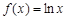 ,
,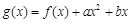 ,其中函数
,其中函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于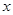 轴.
轴.
(1)确定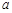 与
与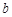 的关系;
的关系;
(2)若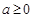 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(3)设斜率为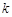 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点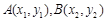
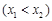 ,求证:
,求证: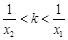 .
.