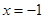如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F= ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2-GB2=DF•GF.
如图,在平面直角坐标系中,反比例函数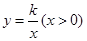 的图象和矩形ABCD在第一象限,AD平行于
的图象和矩形ABCD在第一象限,AD平行于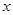 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标.
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE
(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.
已知正比例函数 和反比例函数的图象交于点A(m,一2).
和反比例函数的图象交于点A(m,一2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量 的取值范围;
的取值范围;
(3)若双曲线上点c(2,n)沿OA方向平移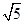 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
如图,在□ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.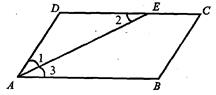
(1)求EC的长;
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形
先化简,再求值.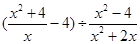 ,其中
,其中