某建筑工地决定建造一批简易房(房型为长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内.
(1)设房前面墙的长为x,两侧墙的长为y,所用材料费为p,试用x,y表示p;
(2)简易房面积S的最大值是多少?并求当S最大时,前面墙的长度应设计为多少米?
(本 小题14分)已知函数
小题14分)已知函数 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称
(1)求函数 的解析式;
的解析式;
(2)若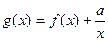 ,
, 在区间
在区间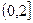 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围.
(本小题13分)某饮料生产企业为了占有更多的市场份额,拟在2010年度进行
一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件
饮料需再投入32万元的生产费用,若将每件饮料的售价定为:其生产成本的150%与平均
每件促销费的一半之和,则该年生产的饮料正好能销售完。
(1)将2010年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)


(本小题12分)已知向量 .
.
(1)若 ‖
‖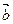 ,求
,求 ;
;
(2)当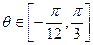 时,求
时,求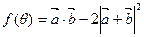 的最值。
的最值。