在如图所示的多面体ABCDE中，AB∥DE，AB⊥AD，△ACD是正三角形，AD=DE=2AB=2，
，F是CD的中点．
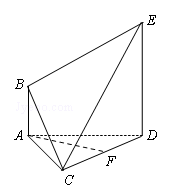
（Ⅰ）求证AF∥平面BCE；
（Ⅱ）求多面体ABCDE的体积．
在棱长为2的正方体ABCD—A1B1C1D1中，E为棱AB的中点，点P在平面A1B1C1D1内，若
D1P⊥平面PCE，试求线段D1P的长。
已知a，b都是正实数，且a+b=2，求证：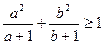
已知函数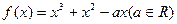
（1）当a=0时，求与直线x-y-10 =0平行，且与曲线y=f(x)相切的直线的方程；
（2）求函数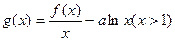
的单调递减区间；
（3）如果存在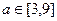
，使函数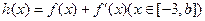
在x=-3处取得最大值，试求b的最大值。
设等比数列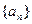
的前n项和为Sn，已知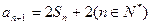
（1）求数列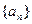通项公式；
（2）在
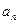与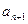
之间插入n个数，使这n+2个数组成一个公差为
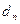的等差数列。
（Ⅰ）求证：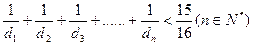
（Ⅱ）在数列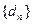
中是否存在三项
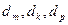（其中m，k，p成等差数列）成等比数列，若存在，求出这样的三项；若不存在，说明理由
在平面直角坐标系xoy中，已知定点A（-4，0），B（4，0），动点P与A、B连线低斜率之积为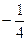
。
（1）求点P的轨迹方程；
（2）设点P的轨迹与y轴负半轴交于点C，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得弦长为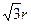
。
（Ⅰ）求圆M的方程；
（Ⅱ）当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如
果不存在，说明理由。