(本小题满分13分)如图: 是直径为
是直径为 的半圆,
的半圆,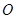 为圆心,
为圆心,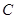 是
是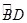 上一点,且
上一点,且 .
.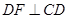 ,且
,且 ,
, ,
, 为
为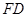 的中点,
的中点, 为
为 的中点,
的中点,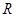 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: 面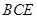 ⊥面
⊥面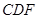 ;
;
(Ⅱ)求证: ∥平面
∥平面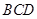 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
已知函数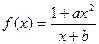
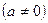 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),
的图像经过点(1,3),
(1)求实数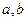 的值;
的值;
(2)求函数 的值域。
的值域。
.已知命题 有两个不等的
有两个不等的 负实根;命题
负实根;命题 无实根,若
无实根,若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围。
的取值范围。
 ,B=
,B= ,全集为
,全集为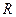 ,
,
(1)求A,B;
(2)求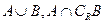 。
。
(本小题满分16 分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
(1)求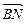 的长;
的长;
(2)求 的值;
的值;
(3)求证:A1B⊥C1M.
(本小题满分16分)甲、乙两人各进行3次射击,甲每次击中目标的概率为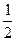 ,乙每次击中目标的概
,乙每次击中目标的概 率为
率为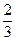 .
.
(1)记 甲击中目标的次数为X,求X的概率分布及数学期望E (X);
甲击中目标的次数为X,求X的概率分布及数学期望E (X);
(2)求乙至多击中目标2次的概率 ;
;
(3)求甲恰好比乙多击中目标2次的概率.