,B=
,B= ,全集为
,全集为 ,
,
(1)求A,B;
(2)求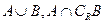 。
。
如图所示的多面体中,  是菱形,
是菱形, 是矩形,
是矩形,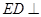 面
面 ,
, .
.
(1)求证:平 ;
;
(2))若 ,求四棱锥
,求四棱锥 的体积.
的体积.
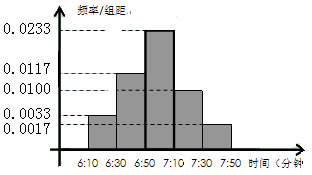
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数 和中位数
和中位数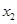 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间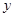 在
在
|
上午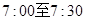 之间,而送报人每天在
之间,而送报人每天在 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件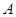 )的概率.
)的概率.
已知函数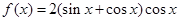 .
.
(1)求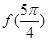 的值;
的值;
(2)求函数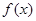 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
设函数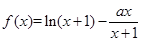 ,
,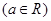 ;
; ,
, .
.
(1)求函数 的单调区间;
的单调区间;
(2)当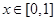 时,求函数
时,求函数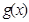 的最大值;
的最大值;
(3)求证: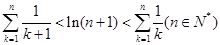
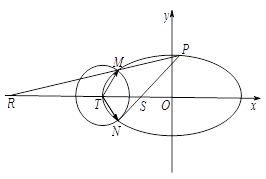
如图,已知椭圆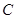 :
: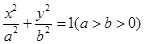 的离心率为
的离心率为 ,以椭圆
,以椭圆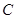 的左顶点
的左顶点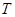 为圆心作圆
为圆心作圆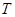 :
: ,设圆
,设圆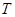 与椭圆
与椭圆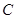 交于点
交于点 与点
与点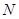 .
.
(1)求椭圆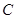 的方程;
的方程;
(2)求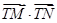 的最小值,并求此时圆
的最小值,并求此时圆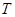 的方程;
的方程;
(3)设点 是椭圆
是椭圆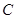 上异于
上异于 ,
,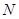 的任意一点,且直线
的任意一点,且直线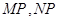 分别与
分别与 轴交于点
轴交于点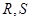 ,
,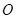 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.