(本小题满分12分)一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如图),
,由此得到样本的重量频率分布直方图(如图),
(Ⅰ)求 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(Ⅱ)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
已知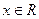 ,
,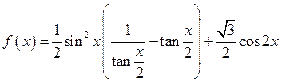 .
.
(1)若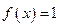 ,求
,求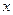 的值.
的值.
(2)若 ,求
,求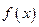 的单调的递减区间;
的单调的递减区间;
某蔬菜基地种植甲、乙两种无公害蔬菜,生产一吨甲种蔬菜需用电力9千瓦时,耗肥4吨;生产一吨乙种蔬菜需用电力5千瓦时,耗肥5吨。现该基地仅有电力390千瓦时,肥240吨。已知生产一吨甲种蔬菜获利700元,生产一吨乙种蔬菜获利500元,在上述电力、肥的限制下,问如何安排甲、乙两种蔬菜种植,才能使利润最大?最大利润是多少?
在 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且 为最大边,
为最大边, .
.
(1)求 的值;
的值;
(2)若 ,求
,求 边长.
边长.
已知等比数列 前
前 项之和为
项之和为 ,
, ,
, ,求
,求 和
和
(本小题满分12分)
有一个容量为50的样本,数据的 分组及各组的频数如下 3;
3; 8;
8; 9;
9; 11;
11; 10;
10; 5;
5; 4.
4.
(1)列频率分布表
(2)画出频率分布直方图
(3)根据频率分布直方图估计数据落在 的概率是多少
的概率是多少