某公司要把240吨矿石运往A、B两地，现用大、小两种货车共20辆，恰好能一次性装完这批矿石.已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往A地的运费为：大车630元/辆，小车420元/辆；运往B地的运费为：大车750元/辆，小车550元/辆.
（1）求这两种货车各用多少辆？
（2）如果安排10辆货车前往A地，其中调往A地的大车有a辆，其余货车前往B地，若设总运费为W，求W与a的关系式（用含有a的代数式表示W）.
（3）在（2）的条件下，如果运往A地的矿石不少于115吨，请你设计出使用总运费最少的货车调配方案，并求出最少总运费？
如图，已知△ABC的三个顶点在格点上.
（1）作出△ABC关于x轴对称的图形△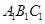
（2）求出△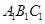的面积.
已知2x－y的平方根为±4，－2是y的立方根，求－2xy的平方根.
如图，二次函数的图象与x轴交与A（4，0），并且OA＝OC＝4OB，点P为过A、B、C三点的抛物线上一动点．
（1）求点B、点C的坐标并求此抛物线的解析式；
（2）是否存在点P，使得△ACP是以点C为直角顶点的直角三角形？若存在，求出点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线，垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
如图，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒．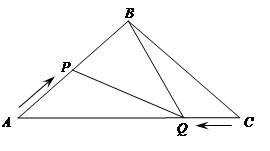
（1）当x为何值时，PQ∥BC；
（2）是否存在某一时刻，使△APQ∽△CQB，若存在，求出此时AP的长；若不存在，请说理由；
（3）当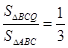
时，求
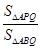的值．
大润发超市以每件30元的价格购进一种商品，试销中发现每天的销售量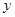
（件）与每件的销售价
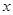（元）之间满足一次函数
.
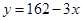（1）写出超市每天的销售利润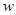
（元）与每件的销售价x（元）之间的函数关系式；
（2）如果超市每天想要获得销售利润420元，则每件商品的销售价应定为多少元？
（3）如果超市要想获得最大利润，每件商品的销售价定为多少元最合适？最大销售利润为多少元？