我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=﹣ (x﹣60)2+41(万元).当地政府拟在“十二·五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q=﹣
(x﹣60)2+41(万元).当地政府拟在“十二·五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q=﹣ (100﹣x)2+
(100﹣x)2+ (100﹣x)+160(万元).
(100﹣x)+160(万元).
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
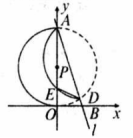
如图,已知直线 ,与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 .
(1)当 时,求 的长;
(2)是否存在实数 ,使沿直线 把弧 翻转后所得的弧与 相切?若存在,请求出此时 的值;若不存在,请说明理由.
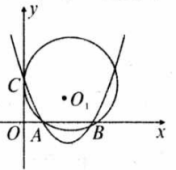
如图所示,在平面直角坐标系中, 与 轴交于 (且 两点,与 轴相切于点 .
(1)求点 的坐标和 的值;
(2)求过点 的抛物线解析式;
(3)若抛物线顶点为 ,判断点 与 的位置关系,并求出 的外接圆半径.
如图①, 为第一象限内一点,过 两点的 交 轴正半轴于点 ,交 轴正半轴于点 .
(1)求证: 平分 ;
(2)作 交弦 于点 .
①若 ,求 的长;
②若 ,把 沿 轴翻折,得到 (如图②),求 的长.

如图, 是 的直径,过点 作 的切线 ,点 在右半圆上移动(点 与点 不重合),过点 作 ,垂足为 .点 在射线 上移动(点 在点 的右边),且在移动过程中保持 .
(1)若 的延长线相交于点 ,判断是否存在点 ,使得点 恰好在 上?若存在,求出 的大小;若不存在,请说明理由;
(2)连接 交 于点 ,设 ,试问: 的值是否随点 的移动而变化?证明你的结论.

如图, 是半圆的直径,弦 ,过点 的切线交 的延长线于点 交 的延长线于点 .求证: .
