(本小题满分16分)心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量记为1,则x天后的存留量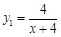 ;若在t(t>4)天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存留量y2随时间变化的曲线恰为直线的一部分,其斜率为
;若在t(t>4)天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存留量y2随时间变化的曲线恰为直线的一部分,其斜率为 (a<0),存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”.
(a<0),存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”.

(1)若a=-1,t=5求“二次复习最佳时机点”;
(2)若出现了“二次复习最佳时机点”,求a的取值范围.
已知点 是抛物线
是抛物线 的焦点.
的焦点.
(1)求抛物线方程;
(2)若点 为圆
为圆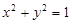 上一动点,直线
上一动点,直线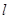 是圆在点
是圆在点 处的切线,直线
处的切线,直线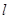 与抛物线相交于
与抛物线相交于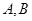 两点(
两点(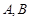 在
在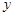 轴的两侧),求平面图形
轴的两侧),求平面图形 面积的最小值.
面积的最小值.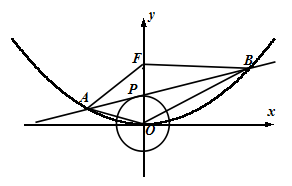
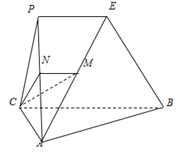
如图,平面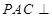 平面
平面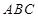 ,
,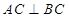 ,
,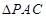 为等边三角形,
为等边三角形, ,过
,过 作平面交
作平面交 、
、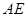 分别于点
分别于点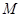 、
、 .
.
(1)求证: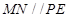 ;
;
(2) 设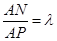 ,求
,求 的值,使得平面
的值,使得平面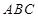 与平面
与平面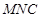 所成的锐二面角的大小为
所成的锐二面角的大小为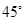 .
.
已知公比 不为
不为 的等比数列
的等比数列 的首项
的首项 ,前
,前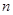 项和为
项和为 ,且
,且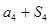 ,
,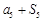 ,
,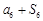 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)对 ,在
,在 与
与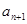 之间插入
之间插入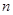 个数,使这
个数,使这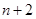 个数成等差数列,记插入的这
个数成等差数列,记插入的这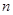 个数的和为
个数的和为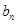 求数列
求数列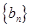 的前
的前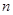 项和
项和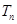 .
.
已知函数 .设
.设 时
时 取到最大值.
取到最大值.
(1)求 的最大值及
的最大值及 的值;
的值;
(2)在 中,角
中,角 所对的边分别为
所对的边分别为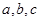 ,
,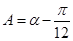 ,且
,且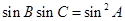 ,
,
求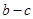 的值.
的值.
已知函数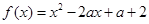 .
.
(1)若 的解集
的解集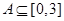 ,求实数
,求实数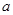 的取值范围;
的取值范围;
(2)若 在区间
在区间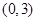 内有两个零点
内有两个零点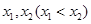 ,求实数
,求实数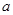 的取值范围.
的取值范围.