已知点 是抛物线
是抛物线 的焦点.
的焦点.
(1)求抛物线方程;
(2)若点 为圆
为圆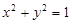 上一动点,直线
上一动点,直线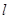 是圆在点
是圆在点 处的切线,直线
处的切线,直线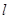 与抛物线相交于
与抛物线相交于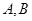 两点(
两点(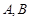 在
在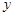 轴的两侧),求平面图形
轴的两侧),求平面图形 面积的最小值.
面积的最小值.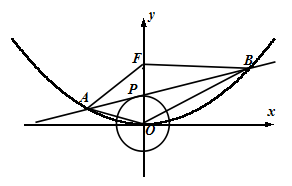
有人统计了同一个省的6个城市某一年的人均国民生产总值(即人均GDP)和这一年各城市患白血病的儿童数量,如下表:
| 人均GDP(万元) |
10 |
8 |
6 |
4 |
3 |
1 |
| 患白血病的儿童数 |
351 |
312 |
207 |
175 |
132 |
180 |
通过计算可得两个变量的回归直线方程为 =23.25x+102.25,假如一个城市的人均GDP为12万元,那么断言:这个城市患白血病的儿童一定超过380人,请问这个断言是否正确?
=23.25x+102.25,假如一个城市的人均GDP为12万元,那么断言:这个城市患白血病的儿童一定超过380人,请问这个断言是否正确?
在数列{an}中,a1=1,an+1= 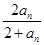 (n∈N*).
(n∈N*).
(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想an,并用数学归纳法证明;
(Ⅲ)若数列bn= 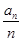 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。
在直角坐标系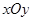 中,点P到两定点
中,点P到两定点 ,
,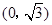 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为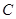 ,过点
,过点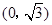 的直线C交于A,B两点.
的直线C交于A,B两点.
(1)写出C的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值,若存在, 求出d的最大值、最小值.
已知函数 在
在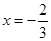 与
与 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数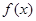 的单调区间
的单调区间
(2)若对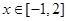 ,不等式
,不等式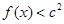 恒成立,求
恒成立,求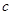 的取值范围
的取值范围
已知函数f(x)= x2+lnx.
x2+lnx.
(1)求函数f(x)的单调区间;
(2)求证:当x>1时, x2+lnx<
x2+lnx< x3.
x3.