某校高三年级一次数学考试之后,为了解学生的数学学习情况,随机抽取n名学生的数学成绩,制成如表所示的频率分布表.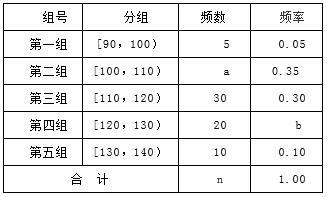
(1)求a,b,n的值;
(2)若从第三、四、五组中用分层抽样方法抽取6名学生,并在这6名学生中随机抽取2名与张老师面谈,求第三组中至少有1名学生与张老师面谈的概率.
已知函数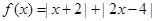
(1)求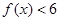 的解集;
的解集;
(2)若关于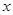 的不等式
的不等式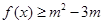 的解集是
的解集是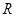 ,求
,求 的取值范围.
的取值范围.
已知平面直角坐标系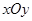 ,以
,以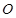 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系,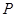 点的极坐标为
点的极坐标为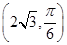 ,曲线
,曲线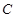 的极坐标方程为
的极坐标方程为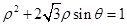
(1)写出点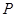 的直角坐标及曲线
的直角坐标及曲线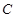 的直角坐标方程;
的直角坐标方程;
(2)若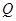 为曲线
为曲线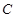 上的动点,求
上的动点,求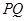 中点
中点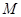 到直线
到直线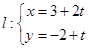 (
(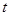 为参数)距离的最小值.
为参数)距离的最小值.
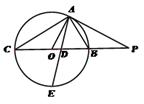
如图所示, 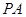 为圆
为圆 的切线,
的切线, 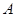 为切点,
为切点,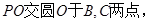
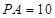 ,
,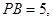
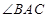 的角平分线与
的角平分线与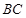 和圆
和圆 分别交于点
分别交于点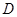 和
和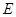 .
.
(1)求证 (2)求
(2)求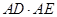 的值.
的值.
已知函数 .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)设 ,证明:对任意
,证明:对任意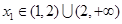 ,总存在
,总存在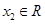 ,使得
,使得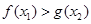 .
.
已知椭圆C的中心在原点,焦点在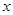 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为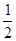
(1)求椭圆C的方程;
(2)设直线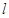 经过点
经过点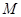 (0,1),且与椭圆C交于
(0,1),且与椭圆C交于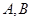 两点,若
两点,若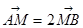 ,求直线
,求直线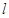 的方程.
的方程.