已知函数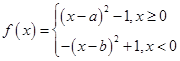 ,其中
,其中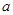 ,
,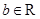 .
.
(Ⅰ)当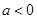 时,且
时,且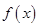 为奇函数,求
为奇函数,求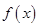 的表达式;
的表达式;
(Ⅱ)当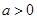 时,且
时,且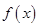 在
在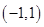 上单调递减,求
上单调递减,求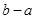 的值.
的值.
已知函数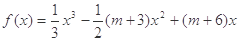 ,x∈R.(其中m为常数).
,x∈R.(其中m为常数).
(1)当 时,求函数的极值点和极值;
时,求函数的极值点和极值;
(2)若函数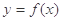 在区间(0,+∞)上有两个极值点,求实数
在区间(0,+∞)上有两个极值点,求实数 的取值范围.
的取值范围.
如图,在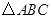 中,
中, ,点
,点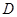 在
在 边上,且
边上,且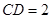 ,
, .
.
(1)求 ;
;
(2)求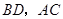 的长.
的长.
设等差数列 的前
的前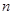 项和为
项和为 ,且
,且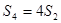 ,
,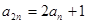 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前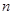 项和为
项和为 ,且
,且 (其中
(其中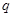 是非零的实数),若
是非零的实数),若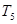 ,
, ,
,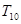 成等差数列,问
成等差数列,问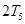 ,
,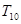 ,
,  能成等比数列吗?说明理由;
能成等比数列吗?说明理由;
(3)设数列 的通项公式
的通项公式 ,是否存在正整数
,是否存在正整数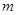 、
、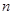 (
(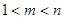 ),使得
),使得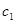 ,
, ,
,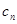 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有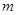 、
、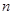 的值;若不存在,说明理由。
的值;若不存在,说明理由。
设函数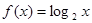 。
。
(1)解不等式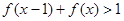 ;
;
(2)设函数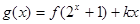 ,若函数
,若函数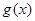 为偶函数,求实数
为偶函数,求实数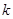 的值;
的值;
(3)当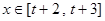 时,是否存在实数
时,是否存在实数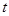 (其中
(其中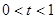 ),使得不等式
),使得不等式 恒成立?若存在,求出
恒成立?若存在,求出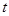 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
对于数列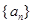 ,如果存在一个正整数
,如果存在一个正整数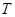 ,使得对任意的
,使得对任意的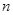 (
( )都有
)都有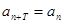 成立,那么数列
成立,那么数列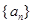 称作周期为
称作周期为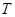 的周期数列,
的周期数列,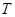 的最小值称作数列
的最小值称作数列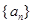 的最小正周期,以下简称周期。
的最小正周期,以下简称周期。
(1)已知数列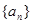 的通项公式是
的通项公式是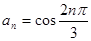 ,判断数列
,判断数列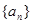 是否是周期数列?并说明理由;
是否是周期数列?并说明理由;
(2)设数列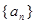 满足
满足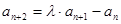 (
( ),
),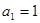 ,
,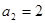 ,且数列
,且数列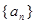 是周期为
是周期为 的周期数列,求常数
的周期数列,求常数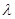 的值;
的值;
(3)设数列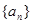 满足
满足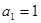 ,
,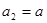 (其中
(其中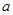 是常数),
是常数), (
( ),求数列
),求数列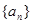 的前
的前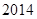 项和
项和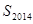 。
。