(本小题满分l2分)
对于定义在区间D上的函数 ,若存在闭区间[a,b]
,若存在闭区间[a,b]  D和常数c,使得对任意x1
D和常数c,使得对任意x1 [a,b],都有
[a,b],都有 ,且对任意x2
,且对任意x2 D,当x2
D,当x2 [a,b]时
[a,b]时 恒成立,则称函数f(x)为区间D上的“平底型”函数
恒成立,则称函数f(x)为区间D上的“平底型”函数
(I)若函数 ="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
="|mx-1|" +|x -2|是R上的“平底型”函数,求m的值;
(Ⅱ)判断函数 =x+|x-l|是否为R上的“平底型”函数?并说明理由;
=x+|x-l|是否为R上的“平底型”函数?并说明理由;
(Ⅲ)若函数g(x)="px+" |x –q|是区间[0,+∞)上的“平底型”函数,且函数的最小值为1,求p,q
的值.
已知
是公差不为零的等差数列,
且
成等比数列
(1)求数列
的通项公式
(2)求数列的前n项和
数列 中, , 是函数 的极小值点.
(Ⅰ)当
时,求通项
;
(Ⅱ)是否存在
,使数列
是等比数列?若存在,求
的取值范围;若不存在,请说明理由.
已知函数
,对任意的
,恒有
.
(Ⅰ)证明:当
时,
;
(Ⅱ)若对满足题设条件的任意
,不等式
恒成立,求
的最小值.
为了考察冰川的融化状况,一支科考队在某冰川上相距8 的 两点各建一个考察基地.视冰川面为平面形,以过 两点的直线为 轴,线段 的的垂直平分线为 轴建立平面直角坐标系在直线 的右侧,考察范围为到点 的距离不超过 区域;在直线 的左侧,考察范围为到 两点的距离之和不超过 区域.

(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图所示,设线段
是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2
,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
如图所示,在正方体 中, 是棱 的中点.
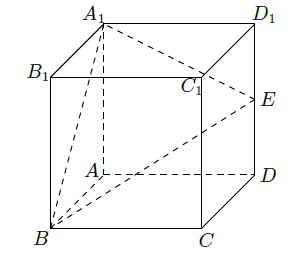
(Ⅰ)求直线
的平面
所成的角的正弦值;
(II)在棱
上是否存在一点
,使
平面
,证明你的结论.