(本小题满分12分)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 .
.
(1)求角C;
(2)若c= ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值.
,求a+b的值.
在直三棱柱ABC-A1B1C1中,△ABC为等腰三角形,∠BAC=90°,且AB=AA1,E、F分别为C1C、BC的中点。
(1)求证:B1F⊥平面AEF
(2)求二面角B1-AE-F的余弦值。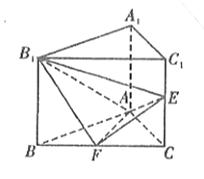
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为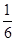 。甲、乙、丙三位同学每人购买了一瓶该饮料。
。甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙没有中奖的概率;
(2)求中奖人数 的分布列及数学期望E
的分布列及数学期望E 。
。
f(x)=sin2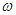 x+
x+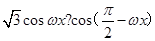 (
(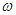 >0),且函数y=f(x)的图象相邻两条对称轴之间的距离为
>0),且函数y=f(x)的图象相邻两条对称轴之间的距离为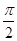 。
。
(1)求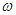 的值及f(x)的单调递增区间;
的值及f(x)的单调递增区间;
已知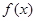 是定义在
是定义在 上的奇函数,当
上的奇函数,当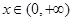 时,
时,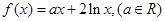
(1)求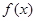 的解析式;
的解析式;
(2)是否存在负实数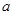 ,使得当
,使得当 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出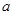 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
(3)对 如果函数
如果函数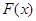 的图像在函数
的图像在函数 的图像的下方,则称函数
的图像的下方,则称函数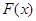 在D上被函数
在D上被函数 覆盖。求证:若
覆盖。求证:若 时,函数
时,函数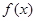 在区间
在区间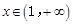 上被函数
上被函数 覆盖。
覆盖。
(本大题13分)设 、
、 为函数
为函数 图象上不同的两个点,
图象上不同的两个点,
且 AB∥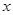 轴,又有定点
轴,又有定点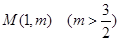 ,已知
,已知 是线段
是线段 的中点.
的中点.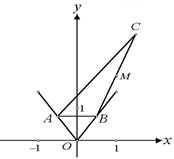
⑴ 设点 的横坐标为
的横坐标为 ,写出
,写出 的面积
的面积 关于
关于 的函数
的函数 的表达式;
的表达式;
⑵ 求函数 的最大值,并求此时点
的最大值,并求此时点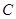 的坐标。
的坐标。